Introduction to the Splitting Patterns and Multiplicity

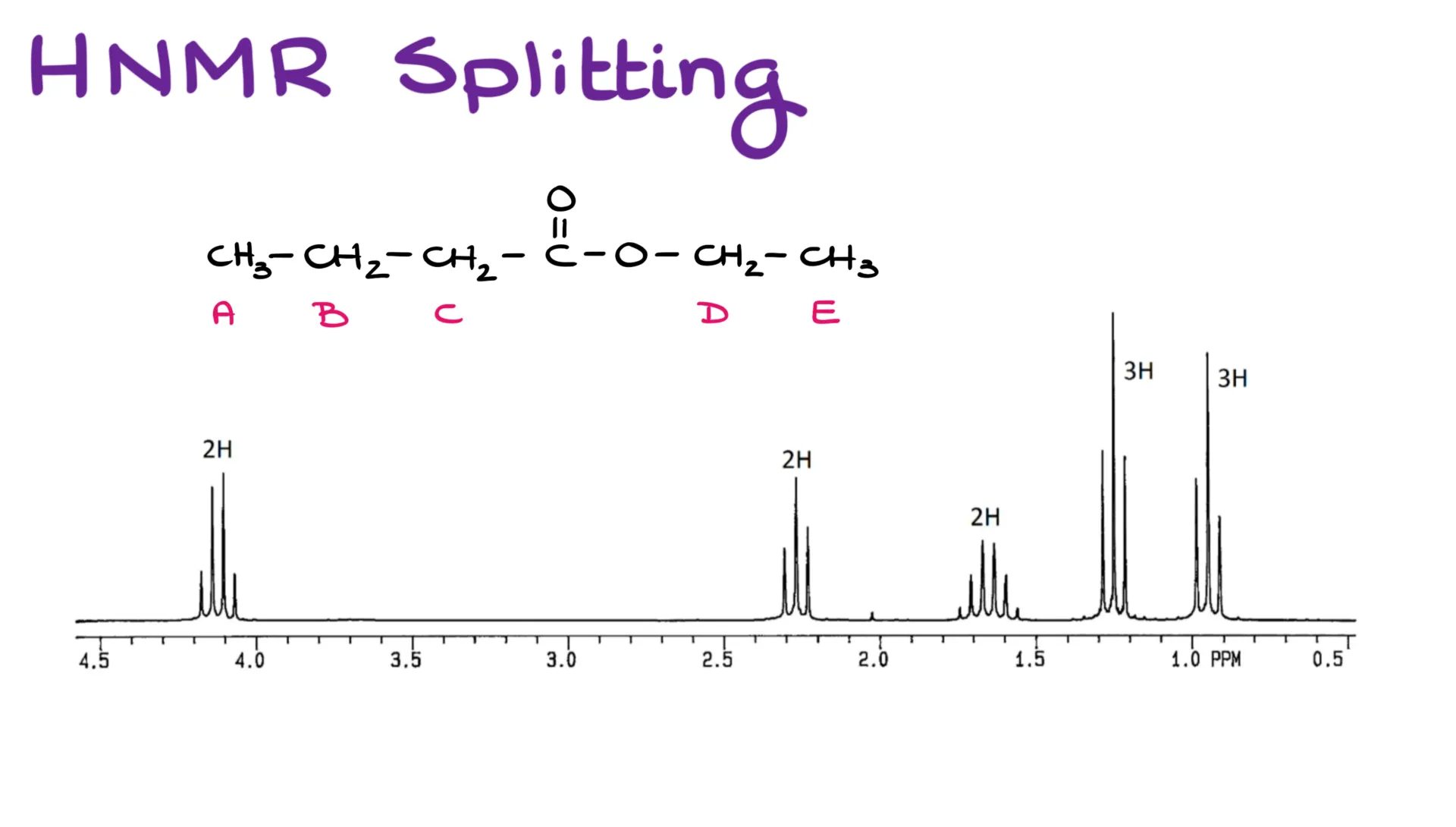
Looking at this spectrum can make anyones head spin. But let’s take it one step at a time and take a close look at what each of those peaks mean and how to interpret those peaks.

In this tutorial I wanna focus on the HNMR splitting patterns, what they mean, where they come from, and most importantly, how to interpret and read them.

Why Do We Have HNMR Splitting?

First of all, why do we have splitting to begin with? If we look at something very simple, like let’s say, ethane molecule, all hydrogens in this molecule are identical. They all have the same connectivity in the molecule like each other hydrogen. They all have the same “magnetic and chemical environment” like each other hydrogen. 

The NMR instrument measures the amount of energy it takes to flip the nuclei’s spin. And since all hydrogens are the same here, it neither takes more nor less energy to cause this flip in either of those hydrogens. So, in the eyes of the NMR, they are indistinguishable. Using the terms of chemical toxicity, we can say that they all are homotopic. And because each hydrogen is indistinguishable from the other one, they all show as a single signal.

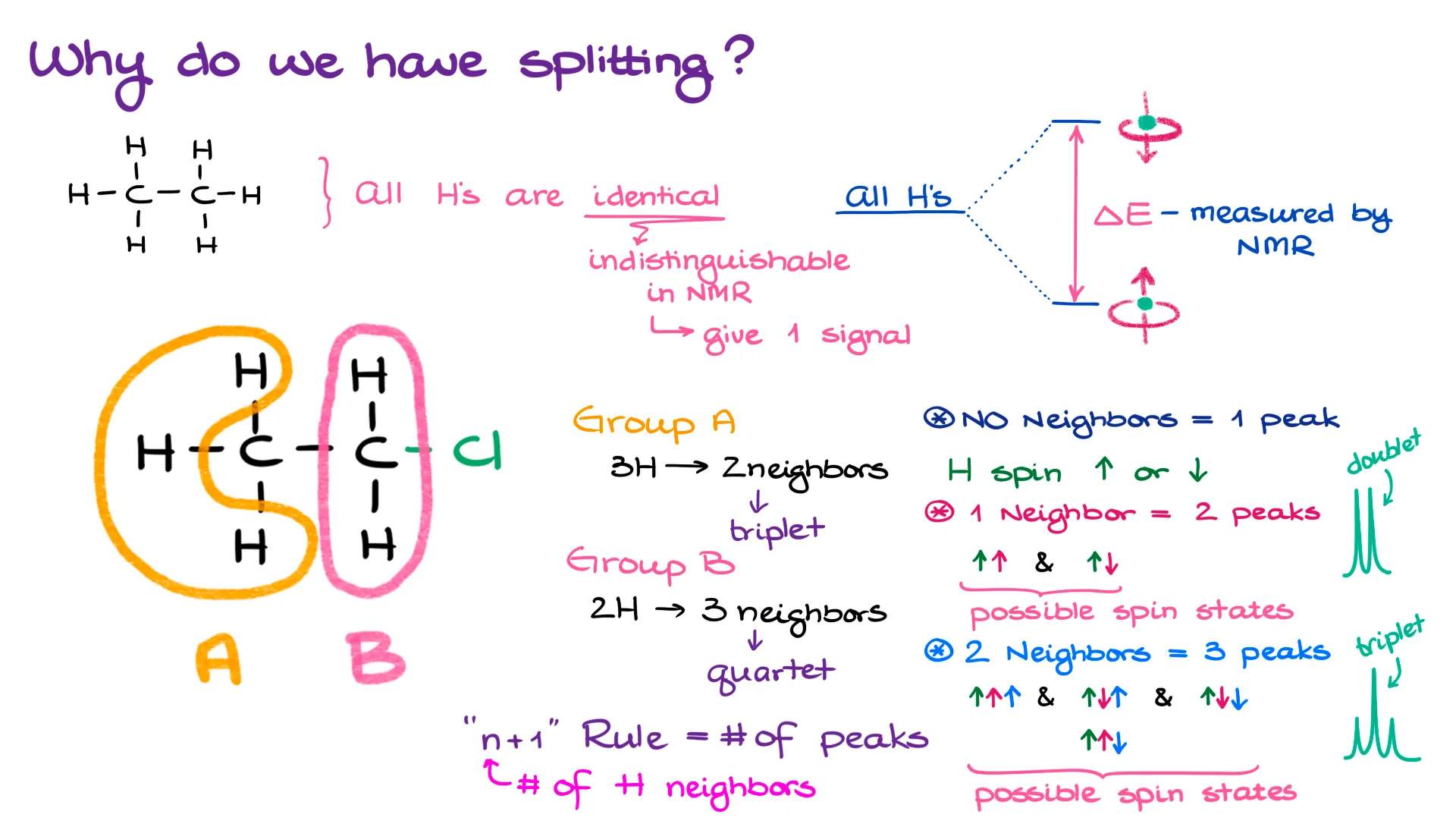
But what happens if I take one of those hydrogens and replace it with, say, a chlorine atom? Now, I have two different groups of hydrogens. One group is the hydrogens of the methyl (CH₃) group. And another group is the methylene (CH₂) hydrogens that are sitting closer to the chlorine atom.

And here’s something very important: since each group of hydrogens is unique now, hydrogens in each group have their own properties including their own minuscule magnetic field. So, they no longer interact with the NMR’s magnetic field in the same way. And on top of that, they have different energy it takes to flip their spins. This will cause the differences in the chemical shifts for the hydrogens in each group.

But because hydrogens in each group have their own slightly different magnetic fields around them, they also start affecting their neighbors in a rather interesting way. Let’s zoom on a single hydrogen from my molecule.

Without any neighbors, it takes a certain discrete energy to flip its spin. The exact energy will determine the hydrogen’s chemical shift which we’ll represent in ppm’s. But the chemical shift is irrelevant to us for the moment. So, I’m not going to focus on that for right now.

We can represent the spin as an arrow. This is a simple quantum mechanical trick that we can use for the bookkeeping purposes. It doesn’t have any specific meaning. We do the same symbolic representation when we’re talking about electrons and their spins. And while I can represent my spin with the up arrow (↑) or a down arrow (↓), I’ll always represent the nucleus of interest with the up arrow.

So, if I go back to my hydrogen of interest here, I’ll say that its spin is the up arrow and its magnetic field aligned with the external magnetic field of the instrument. But what happens if I have a neighbor with its own magnetic field? That’s where things become more interesting!

You see, since the neighbor has its own weak magnetic field, it can either amplify the external magnetic field, or it can diminish it by a very small amount. But no matter how small that amount is, it’s large enough to affect our hydrogen of interest. And now, depending on what the neighbor is doing, it takes either a little more energy to flip the spin or a little less energy to flip the spin. And boom! We have splitting! We’ll call this type of splitting a “doublet.”

On paper, we can represent it as two possible states. One, in which both our hydrogen’s and the neighbor’s spin align (↑↑). And the other one, in which the spins are opposite to each other (↑↓).

The n+1 Rule and the Pascal’s Triangle

Ok, one neighbor splits our signal in two. Got it. Easy so far. But what if we have two neighbors? What then?

Well, let’s examine the possible states that we can get in this case:

1. We can have a state in which all spins align (↑↑↑)
2. We can have two states in which one spin aligns and another one is opposite to our original hydrogen (↑↑↓ and ↑↓↑)
3. And, we can get a state in which both neighbors are misaligned with our original hydrogen (↑↑↓)

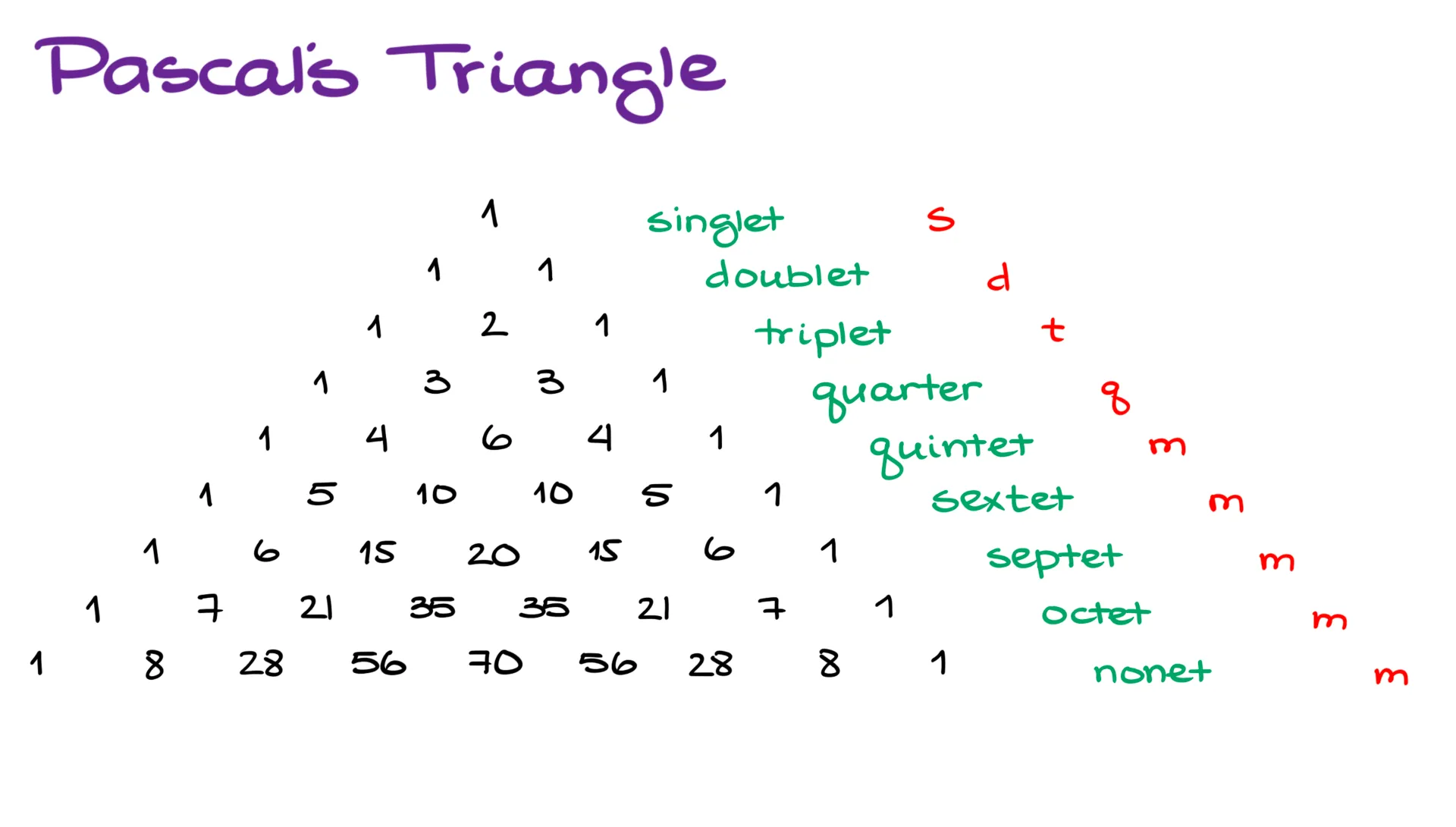
Now, we have three possible energy values that it would take to flip our spin. So, we’ll have a splitting that shows three peaks. We’ll call it a “triplet.” Another interesting observation that we’re going to see in these types of patterns, is that the middle peaks are always going to be much higher than the outer peaks. And the more of those you have, the more of a pyramid shaped signal you’re going to get.

So, how are we going to know the number of peaks that we should expect for each signal? Certainly, we’re not going to be sitting there and looking for all possible spin states every single hydrogen. You’ll either fall asleep or get straight to the loony bin. And despite what you might be thinking about organic chemists, that’s not our intention in the slightest. Luckily for us, we can easily calculate the number of peaks in the signal using the “n+1” formula, where “n” is the number of your neighbors.

And coming back to my molecule, I have two groups of hydrogens here. I’ll call them Group A and Group B. We’re always going to treat a group as a whole entity. And that’s because each group gives a combined signal. Here, we’ll have Group A, that gives one signal, and we have Group B, that gives another signal in our NMR.

Group A “sees” two neighbors that is hydrogens B. Using the “n+1” formula, that gives us 3 peaks in the signal, or a triplet. Group B “sees” three neighbors that is hydrogens A. Using our “n+1” rule again, we’ll get 4 peaks in the signal, or a quartet.

In addition to the “n+1” rule, that allows us to predict the number of peaks in each signal, we can also easily predict the intensity of those signals. For as long as your signals don’t overlap, the signal intensities will correspond to the numbers in the Pascal’s triangle. You might recall this triangle from your algebra classes if you have already covered the binomial distributions.

Examples

So now, when we have a better idea about the splitting and how it works, let’s look at a few examples. The first example I have here is the HNMR spectrum for the methyl butanoate molecule.

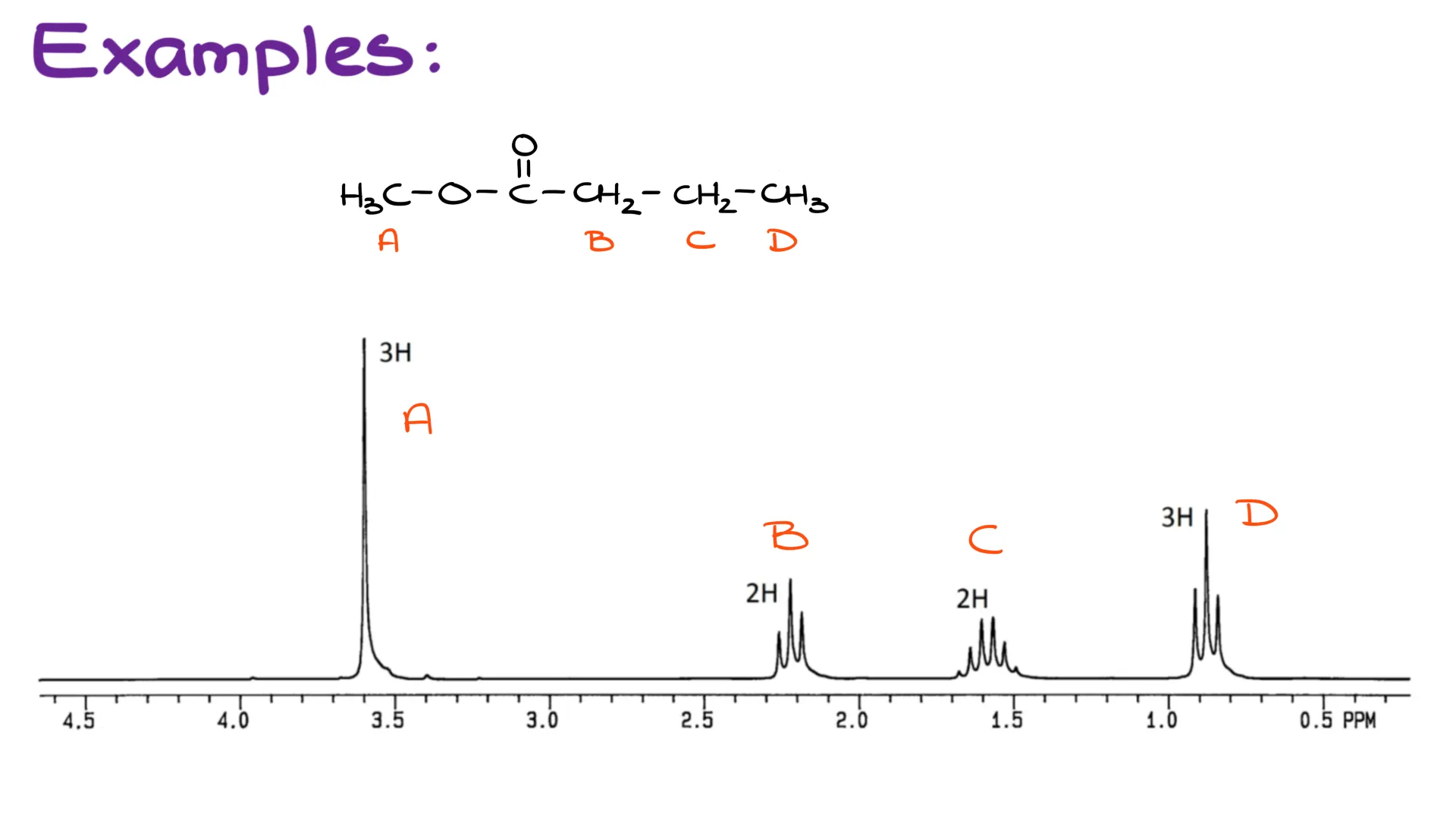
I’m going to label all my groups of hydrogens as A, B, C, and D. Here, we can see that group A has no neighboring hydrogens on the adjacent atom. Thus, it’s a singlet.

The group B has two neighbors, so it’s a triplet.

Now, when it comes to my group C, this one is a bit more complicated. We have two neighboring hydrogens on the left from it (group B), and three more neighboring hydrogens to the right (group D). So, the total number of my neighboring hydrogens is going to be 5, making this signal into a sextet. Typically, anything more than four (aka, quartet) is referred to as a multiplet. However, in this tutorial I’m still going to be naming all those multiplets appropriately for the clarity’s sake.

An important thing to keep in mind is that you should only be looking at the neighboring hydrogens on the adjacent atom. Sometimes, instructors refer to this as an atom “3 bonds away” or something similar to this. If you have hydrogens on atoms further away, they are too far for us, so we are not going to be looking at them at all. There are, of course, cases when hydrogens can interact with each other through space when they are more than 3 bonds away. However, we’re not going to see examples like that in the sophomore organic chemistry course.

Be Mindful of Symmetry

Another important aspect of the NMR is symmetry. You might have a molecule which has a plane of symmetry going through the middle of it. Or maybe just a portion of our molecule is symmetrical.

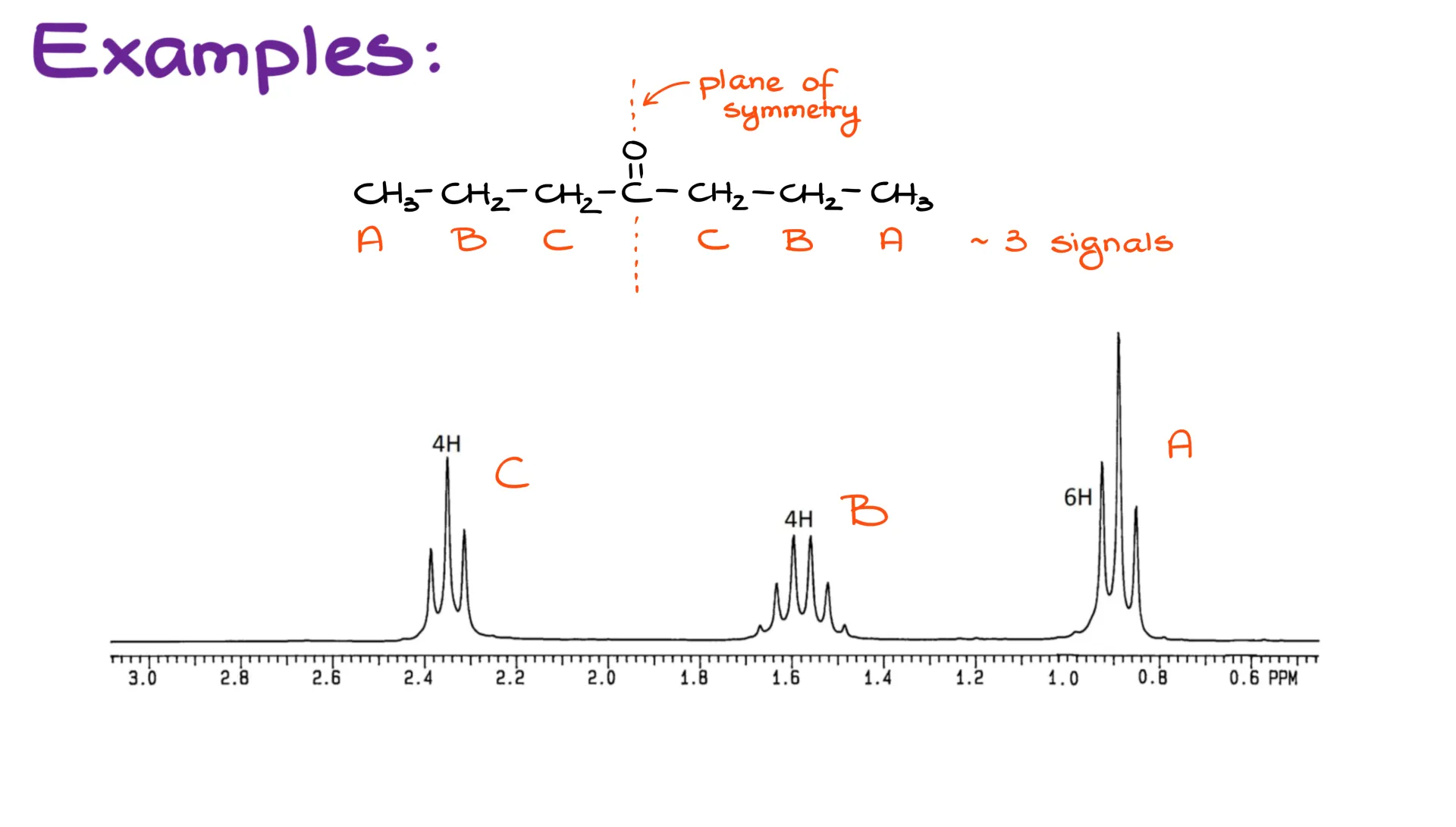
In this case, the identical groups on the opposite sides of the plane of symmetry will show up as a single signal. For instance, let’s look at the HNMR spectrum coming from heptan-4-one.

This molecule has an internal plane of symmetry. And because of that the groups on the right are going to be identical to the groups on the left. So, I’ll call them groups A, B, and C. Overall, this means that our molecule will only have 3 signals. And more importantly, when we’re analyzing the splitting pattern for it, we’ll consider what each group has as neighbors.

So here, each group A has group B as the neighbor. Since each group B has 2 hydrogens, group A will be a triplet.

Likewise, each group B sees A and C as neighbors. We have 3 hydrogens in each group A and 2 hydrogens in each group C, giving us 5 neighboring hydrogens combined for each group B. Thus, our group be, similar to the previous molecule, will be a sextet.

Common Mistake

And before we move to the next example, I wanna point out a common mistake that a lot of students unfortunately make. The “n+1” rule works for predicting the number of peaks for each signal when we’re looking at our molecular structure and trying to predict the spectrum’s shape. However, most of the time you’re going to be doing quite the opposite. You’ll have the spectrum in from of you, and you’ll need to decipher it. And there’s something important that you need to keep in mind here. If you’re looking at the spectrum, you’re going to be using your “n+1” rule in reverse. If you see a quartet, it means you your group has 3 hydrogen neighbors. If you see a doublet, you have one neighbor. If you see a singlet, you have no neighbors.

OH and NH Groups Do NOT Split

Let’s move on to the next example.

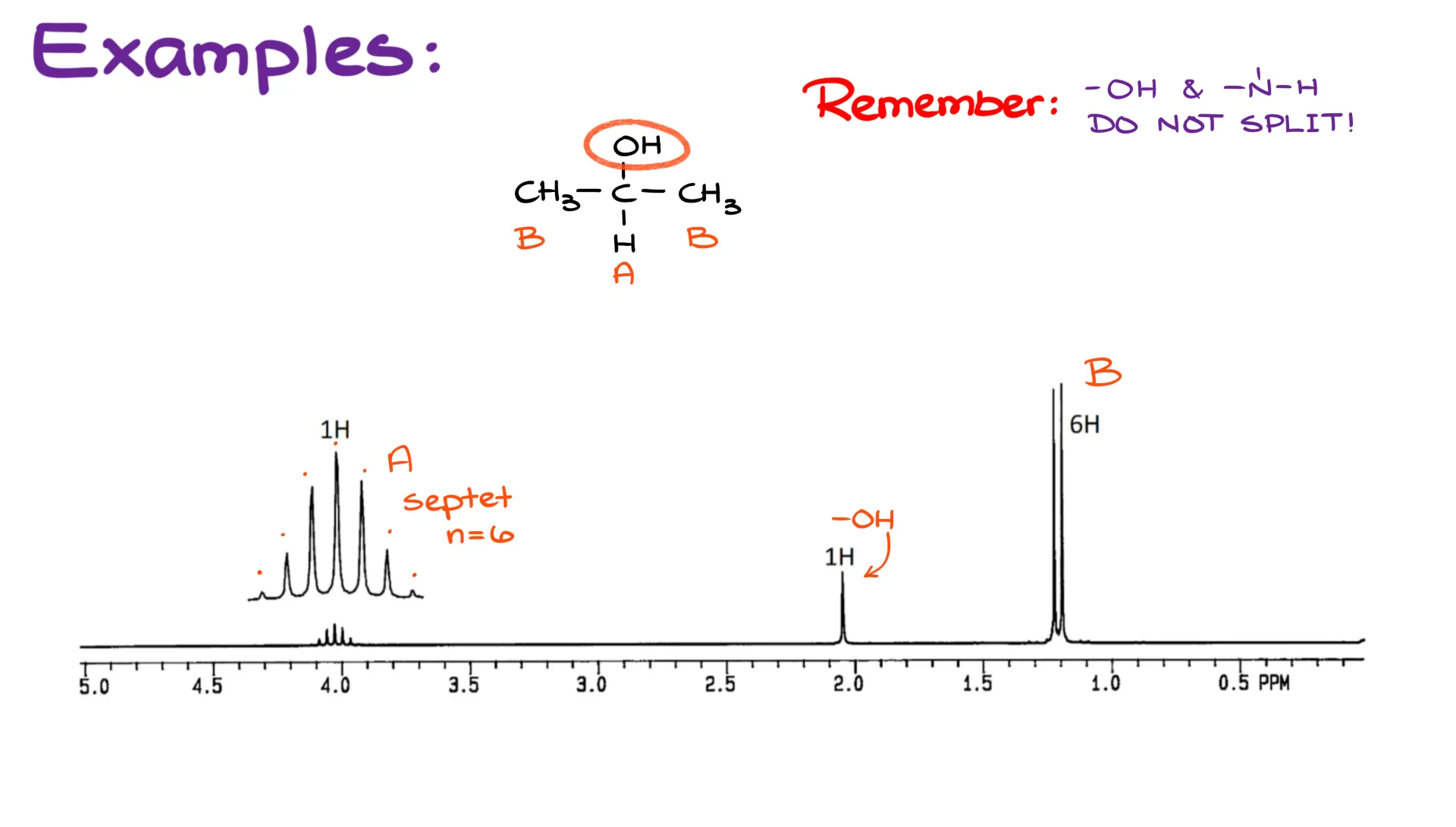
Here, I have a spectrum of isopropanol—a simple 3-carbon alcohol. You probably have a bottle of it in your home medical aide kit since isopropanol is commonly used as a rubbing alcohol for disinfection purposes.

If we closely analyze the spectrum, we’ll see a couple of interesting inconsistencies here. Firstly, if we look at the signal coming from the hydrogen of the -OH group, we’ll see that it’s a singlet. But we do have a hydrogen on the adjacent carbon. And remember, we’re talking about the HNMR, so we’re looking at hydrogens. It doesn’t matter what those hydrogens are attached to. So, don’t make a mistake assuming that if your hydrogen is not sitting on a carbon, it’s irrelevant. But I digress. Looking back at my molecule here, I see a problem. We have just spent a fair amount of time talking about how neighboring hydrogens split. And here, all of a sudden, we’re not seeing any splitting. How come?

Well, without going too deep into details here, the hydrogen bonding that we have in alcohols is to blame. Any hydrogen that can freely participate in hydrogen bonding will neither show any splitting pattern itself, nor will it split neighboring hydrogens. We typically see this phenomenon for alcohols and amines. So here, the -OH gives you a singlet, and the hydrogen C gives you a septet (7 peaks) as if it has no -OH to split from.

Also notice, that although we have two groups B, they both are neighbors to the group C, which means that we have to count all those hydrogens in our splitting. Symmetry can be tricky, so always stay vigilant, otherwise you may miscount your atoms and interpret your spectrum incorrectly.

Complex Spectrum

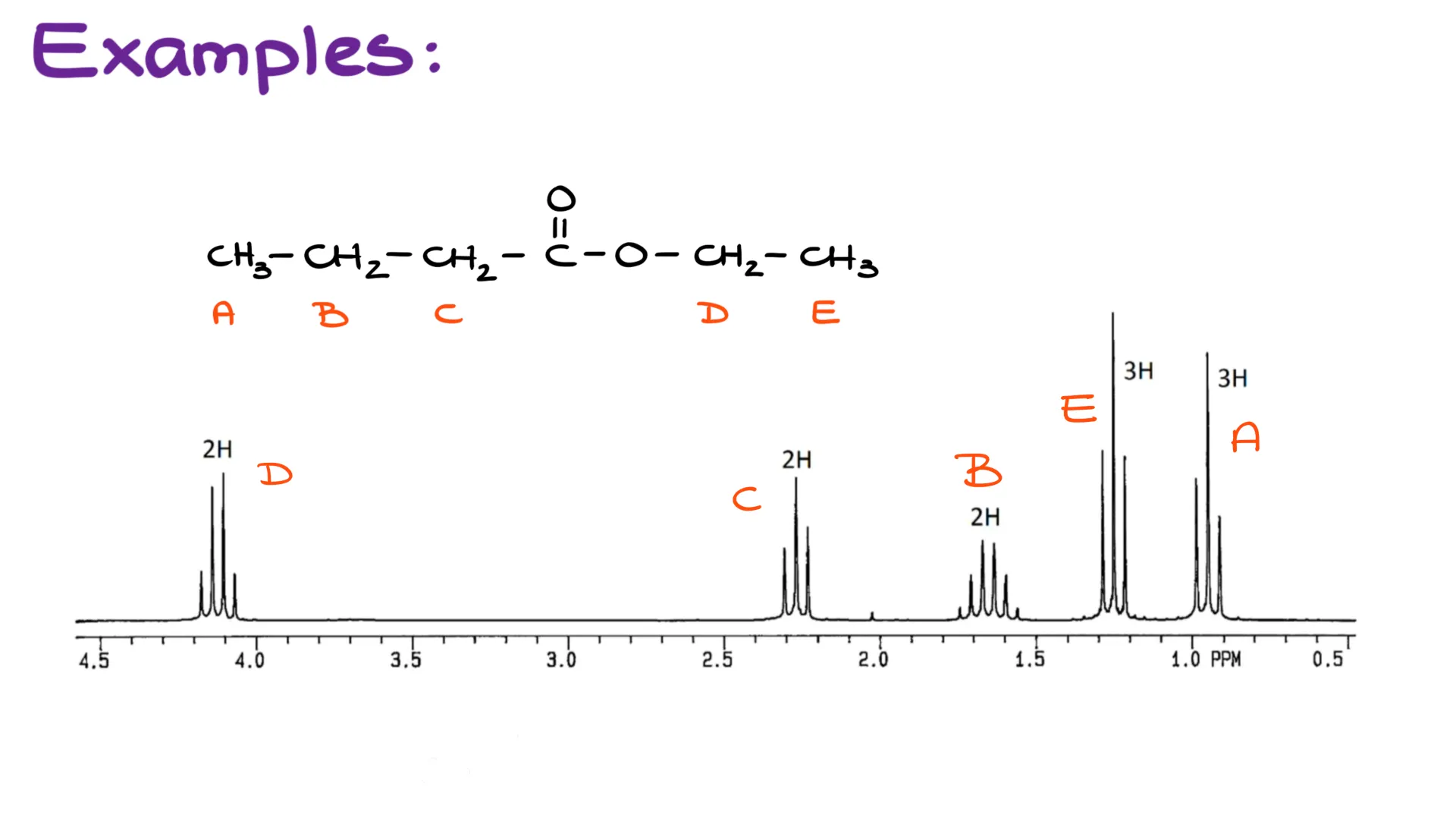
Finally, I wanna circle back to the spectrum that I showed you at the very beginning of this video. It is a large and complex spectrum. However, we can now diligently go through the groups and see how many neighbors we have for each and why each group gives you the signals you’re seeing here. Pause the video and copy the molecule down if you need to and explain back to yourself how each of these groups match up with the spectral data on the screen.

Concluding Thoughts

All the examples that we’ve discussed today are what we call a “first order splitting” and this is the most common splitting pattern type you’re going to see in your course. This is, of course, not all. We can also have complex splitting which is a whole different game, but that’s a topic for a different conversation.

But for now, I want to encourage you to do as much practice as possible.