Converting Between Fischer, Haworth, and Chair Forms of Carbohydrates

In this post I want to go over the three most typical forms of the carbohydrates: Fischer projection for the open-chain molecules, Haworth projections focusing on cyclic pyranoses, and your regular chair conformations. While other structures are possible (and you’re definitely going to encounter them in your course), I’m specifically going to be focusing on the:

• Aldohexoses: carbohydrates that have an aldehyde functional group and contain six carbons. Examples of aldohexoses are glucose and galactose which are essential for the living organisms on Earth.
• Pyranoses: six-membered cyclic structures that result from the hemiacetal formation between the aldehyde on the 1st carbon in the molecule and the -OH group on the 5th carbon.

If you’re not sure what exactly these terms mean, I go over the fundamental nomenclature of carbohydrates in this blog post over here. You might wanna check it out before you continue with this post so you don’t get lost in the discussion when I use the terminology.

Why focusing on the aldohexoses and pyranoses specifically? Glucose, galactose, and mannose are among the most common carbohydrates in living cells. Also, six-membered cyclic forms (pyranoses) are also prevalent in nature, so they are very important. Finally, this is a very typical type of an exam question! So you wanna make sure you really know how to convert Fischer to Haworth and chair and back. You’ll also need to know it for the MCAT even if your organic chemistry professor doesn’t cover it in class. You’ll also cover this topic in any introductory biochemistry class. Carbohydrates is a typical mid first semester biochemistry topic.

Fischer Projections

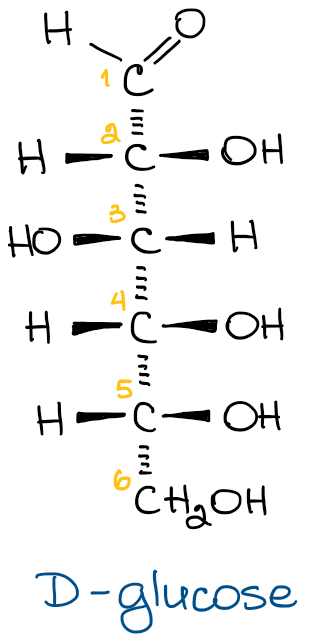
As you probably know, Fischer projections are a very convenient way of drawing a long-chain molecule with a lot of chiral carbons, such as a carbohydrates. In a Fischer projection, we put the most oxidized atom (an aldehyde function) on the top and the rest of the chain following from there. For example, look at the structure of glucose drawn out in the Fischer projection form.

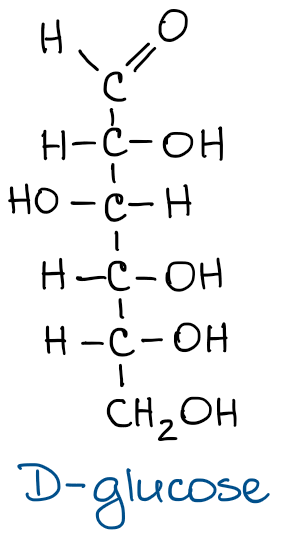
On the left, you have a glucose structure in the Fischer projection with the stereochemistry shown. Every vertical line in the Fischer projection is oriented away from the observer, every horizontal line looks toward the observer. Since this is a common stereochemical convention, we don’t need to show it every single time for the simplicity sake.

What’s important though, is to remember this convention at all times. This means, that Fischer projections CANNOT be flipped in space around their vertical axis as this would make an enantiomer of the molecule! So while we might be drawing it “flat” it actually is not and needs to be treated like a 3D object.

When it comes to the 3D representation of the Fischer projections, I really like the image of a caterpillar standing on its hind legs, bending backwards, while trying to hug you. Let me illustrate what I’m trying to describe here:

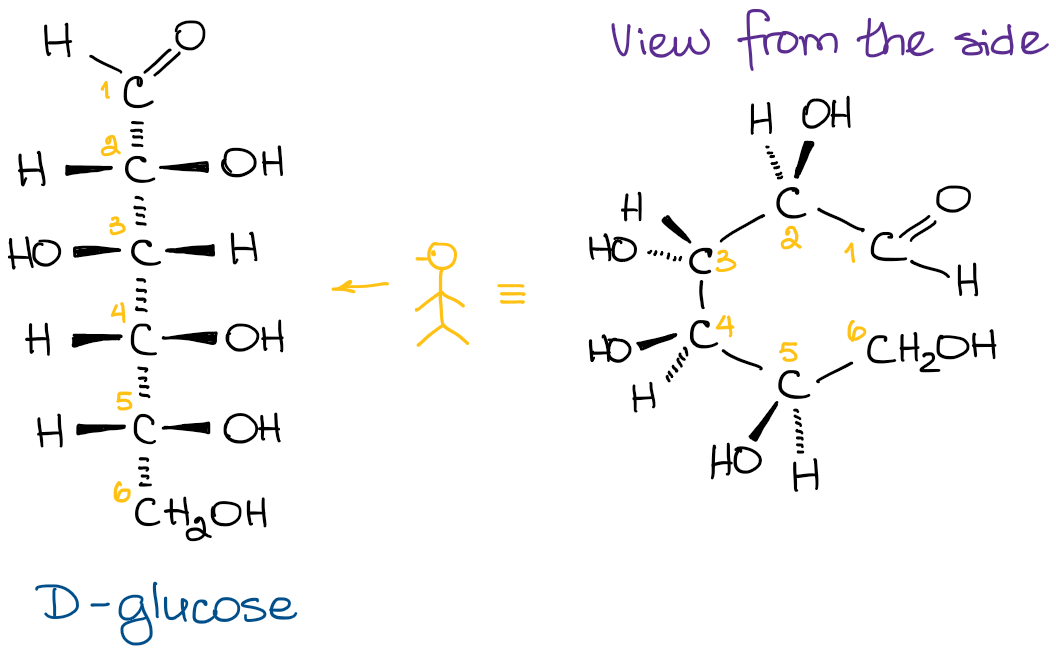
I’m assuming you’re somewhat familiar with the Fischer projections and this all is just a refresher. So, let’s look at how you can convert the Fischer projection into Haworth projection.

Haworth Projections

As I’ve mentioned at the beginning of this post that I’m only going to be focusing on the pyranoses here. Pyranose is a 6-membered ring that is traditionally drawn with the anomeric carbon to the right:

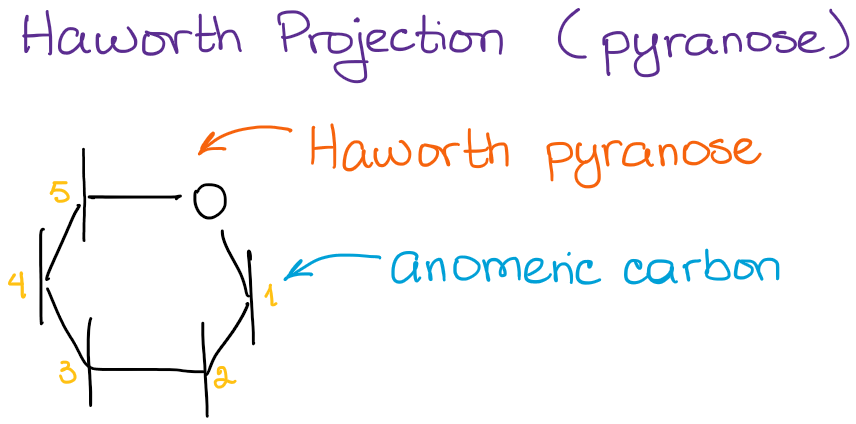
In this type of a representation, we assume that the bottom of the structure is oriented towards the observer. This way, we don’t have to show it with the wedges every single time.

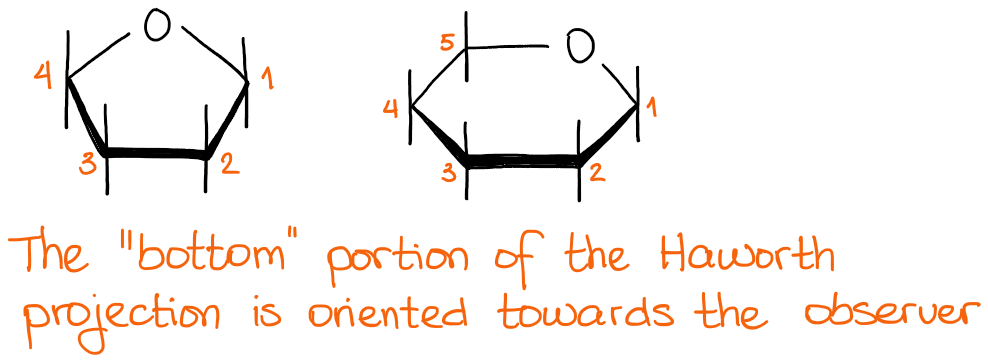
Drawing Haworth projection in a different way might be ambiguous. So if you have to flip it around in some sort of a way to, maybe, make a disaccharide or something like that, please, remember to show the stereochemistry! While this might be a small thing, it CAN cost you some points on the exam. I can tell you from the perspective of an instructor: every time I have to guess, I take off points in my classes. So make your (and your instructor’s) life easier and show the wedges if you draw your molecule in ANY way that is not a canonical/traditional representation.

Steps for Converting Fischer to Haworth

Now, to make a cyclic hemiacetal from your linear Fischer projection, you’ll need to follow a few simple steps:

1. Draw a Haworth’s “stem” like in the picture above
2. Number your atoms 1 through 5 starting from the anomeric carbon and going clockwise
3. If your sugar was D, then the carbon #6 is going to be looking “up” (down for the L sugar)
4. The “right” groups on carbons 2, 3, and 4 in the Fischer projection go onto the “bottom” positions in Haworth
5. The “left” groups on carbons 2, 3, and 4 in the Fischer projection go onto the “up” positions in Haworth

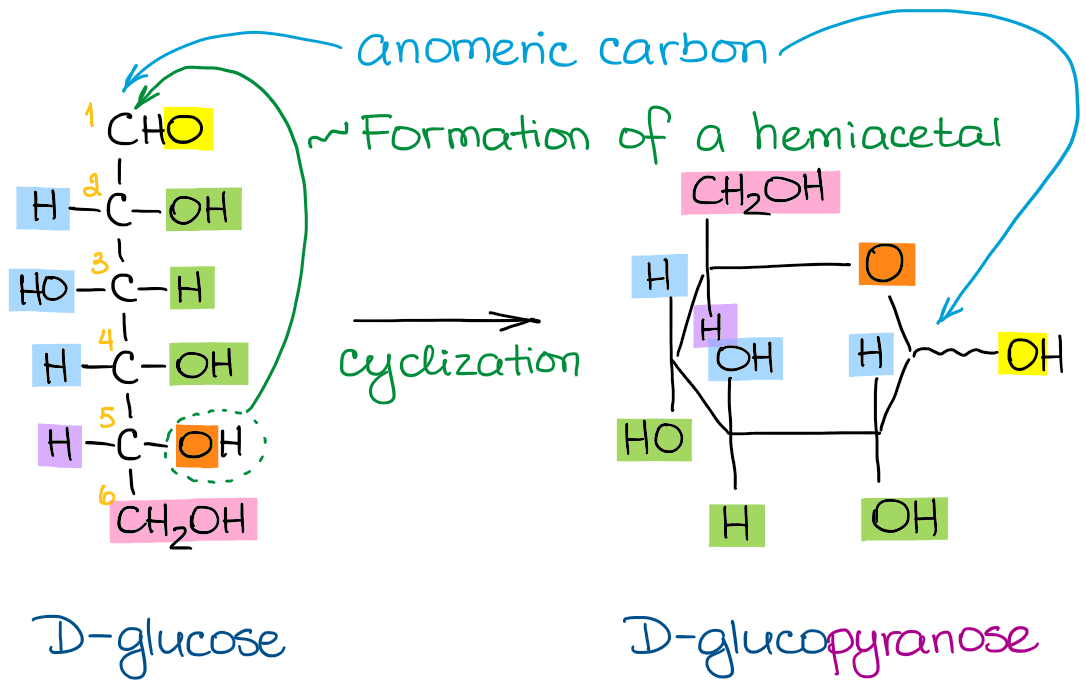
This might sound like a long sequence of steps, but it’s actually a fairly simple process once you get a hang of it. Let’s look at a few more examples to make it a little easier for you to practice the steps. For this exercise, I want to compare the structures of D-glucose, L-idose, and L-glucose:

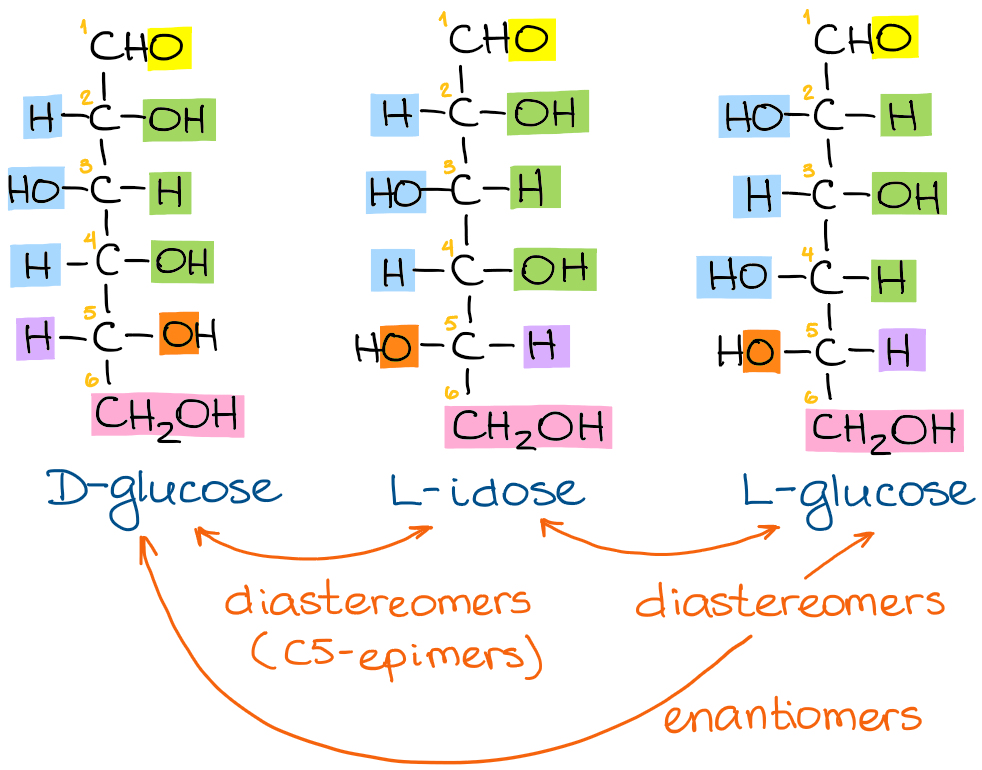
Using the steps from above we get the following Haworth projections:

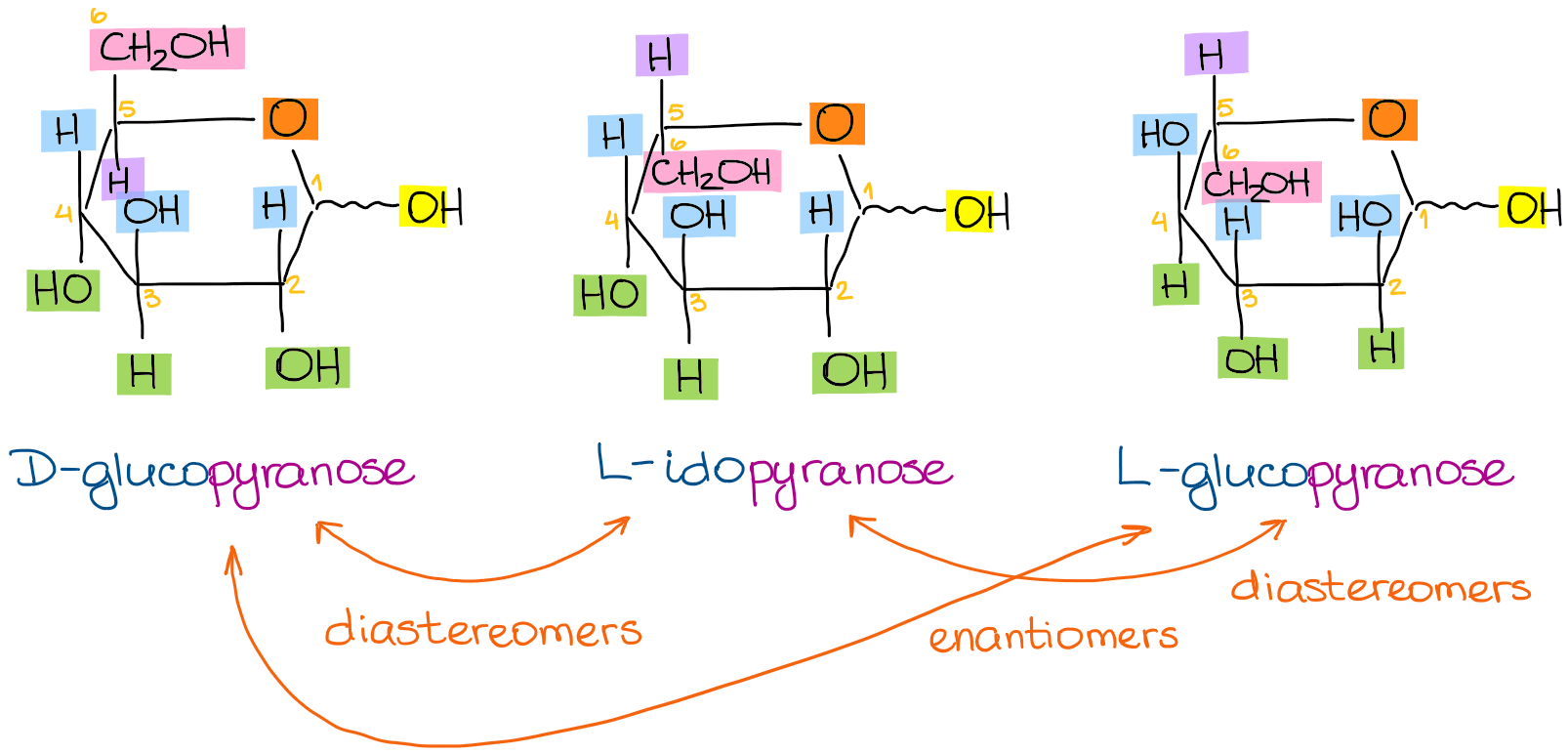
I kept the same color scheme to make it a little easier to see what’s going on and track the groups as we go from one structure to another.

The Stereochemistry of the Anomeric Carbon (the α-form or the β-form)

By now I have defined every stereocenter in the molecule except for the anomeric carbon. The anomeric carbon has a special place in the chemistry of carbohydrates because it doesn’t have a set stereochemistry. This means that it can be either facing “up” or “down” depending on how the cyclization happened. While, there are factors that can make one orientation more favorable than the other one, I’m not going to go over those here to keep this post as much to the point as possible. If you’re curious about the stability of the anomeric -OH in the “up” or a “down” position, look up “anomeric effect” to dive into the topic deeper.

Usually, you can put the anomeric -OH in any position you like. However, some instructors will specify the stereochemistry of the anomeric carbon as either the α-form or the β-form. By the definition, for a pyranose saccharide, the α-form is the one where the anomeric -OH and the carbon #6 are trans to each other, while the β-form has those two groups in a cis configuration.

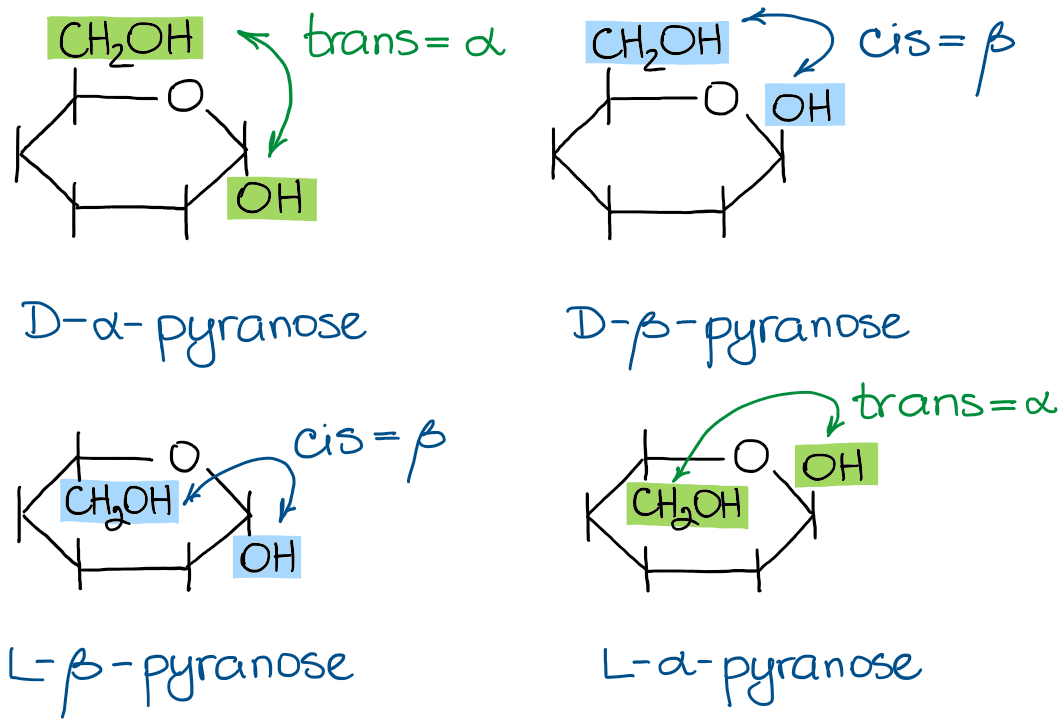
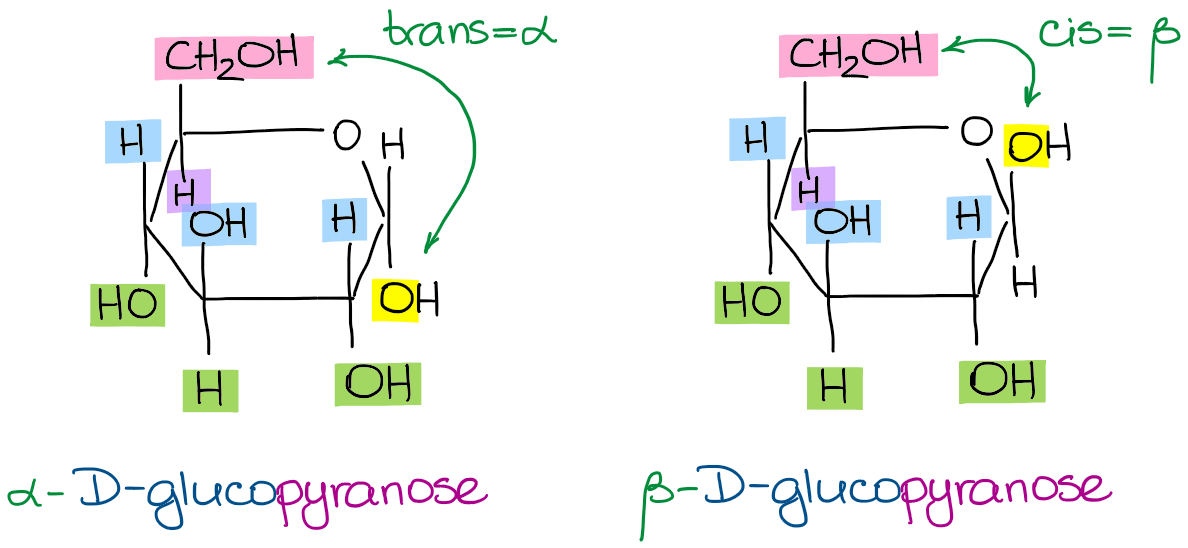
Thus, I can draw either the α- or the β-forms of any of my molecules from above. For instance, here are the α-D-glucopyranose and the β-D-glucopyranose:

Please, pay close attention to what your instructor is asking you on the test! Those little pesky α’s and β’s can cost you a lot of points!

Converting Haworth to Chair

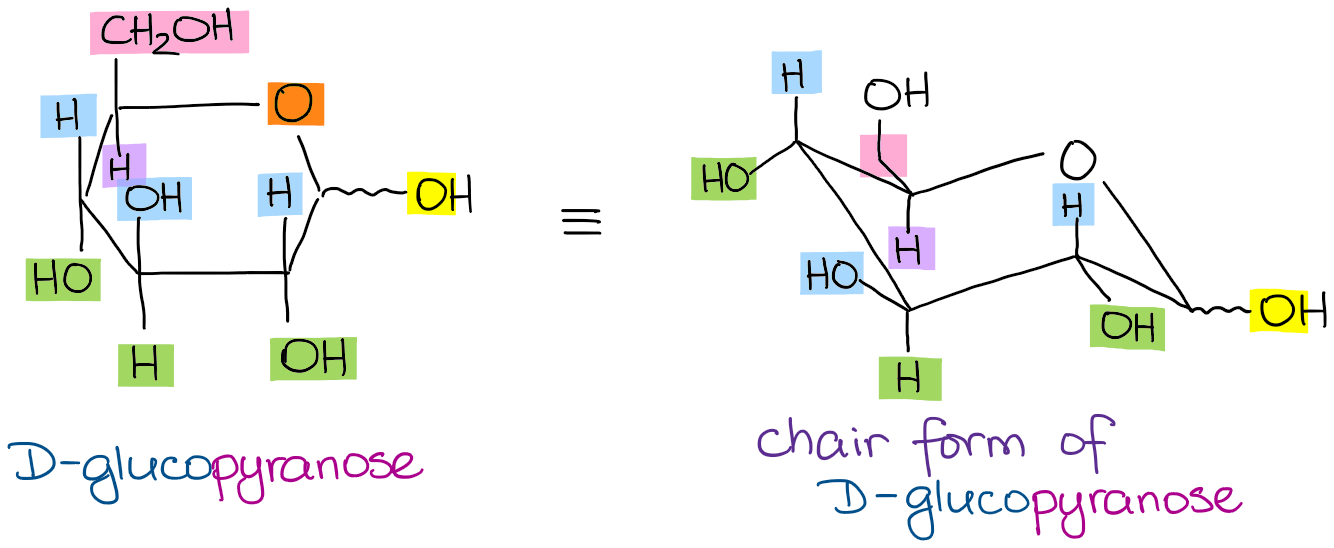
The final piece of these conversions is often to draw a complete chair conformation of the pyranose. The trick is to remember that just like the Haworth projections, the chair conformations also have the well-defined “up” and “down” positions!

Looking at the glucopyranose from above, you now can easily draw the chair conformation for it in a general form:

And, just as easily, you can show a chair conformations specifically for the α-D-glucopyranose and the β-D-glucopyranose:

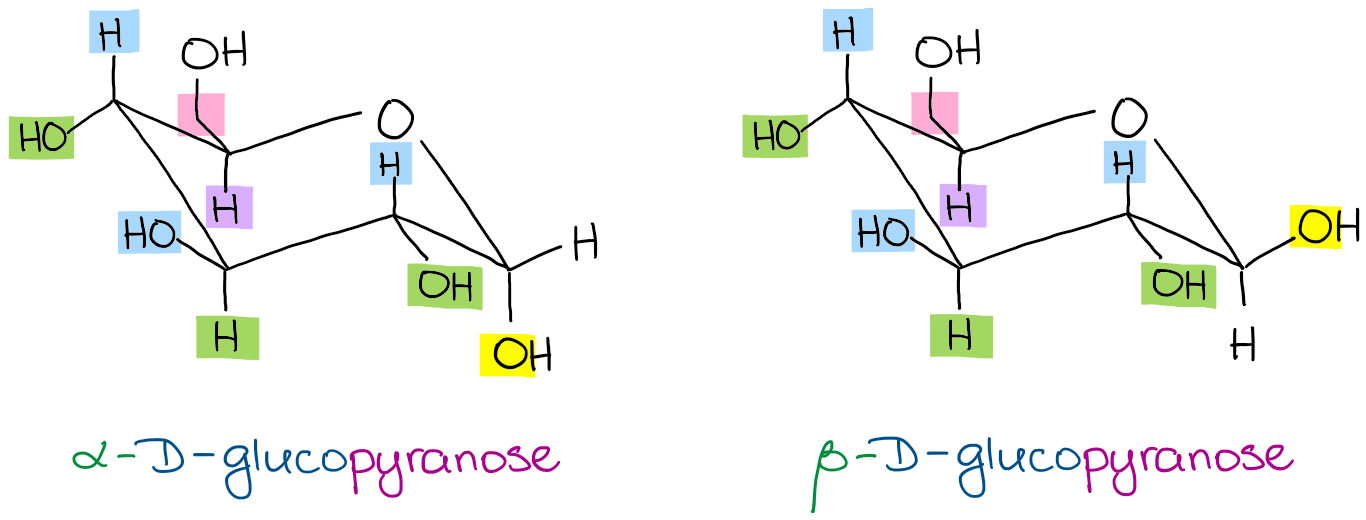
So, for as long as you can properly draw the substituents’ positions in your chair conformation, you should be able to easily convert Haworth to chair! Surprisingly, but a lot of instructors skip the Haworth projections. If your instructor didn’t cover those, I still highly recommend you learn those as they come in handy as a middle step in the Fischer to Haworth to chair conversions. You’ll also need to know those for your MCAT, DAT, PCAT, or other post secondary standardized tests.

This pretty much summarizes a clean and straightforward method of converting from Fischer projection to Haworth projection, to chair conformation for your typical aldohexoses. Occasionally, instructors will ask you to do the opposite and convert from the chair to Haworth and Fischer. So, to be ready for the test, make sure you’re practicing the backwards steps too so you don’t get caught off-guard on the exam 🙂